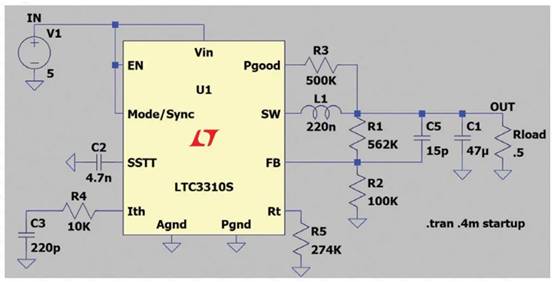
搭档规划一款产品的软件体系完毕了。可是最终几天发现体系不能运用,好像是看门狗一向复位。我试着debug一下,发现确实是看门狗复位形成的。在曾经搭档一向封闭封闭看门狗,在完结一切功用后才翻开的看门狗。所以现在才发现看门狗复位。尽量延伸看门狗复位时刻没有任何作用。所以肯定是某个函数运转时刻太长形成了看门狗复位。在阅读程序后我发现他运用了冒泡排序:
void bubbleSort( int sort[], unsigned char len )
{
char i,j;
int temp;
len -= 2;
for( i =len; i>=0; i–)
{
for( j =0; j<=i; j++)
{
if( sort[j+1] < sort[j])
{
temp = sort[j];
sort[j]=sort[j+1];
sort[j+1]=temp;
}
}
}
}
这是一个典型冒泡排序。假如依照最极点的状况,排序数组sort恰好是反向那么关键字比较次数为n(n-1)/2。移动次数3n(n-1)/2。所以该算法的时刻复杂度应该为n*n。我怀疑是冒泡排序引起的复位后,我屏蔽了该函数运转,产品能够正常运转了。时刻比较紧,体系不能做大的修正,那就只好替换排序算法了。所以我主张选用刺进排序,问题就处理了。产品很快投产上市了。
代码如下:
void insert_sort(int a[],int n)
{
int i,j;
int temp;
for ( i=1; i
{
temp=a[i]; //把待排序元素赋给temp,temp在while循环中并不改动,这样便利比较,而且它是 //要刺进的元素
j=i-1;
//while循环的作用是将比当时元素大的元素都往后移动一个方位
while ((j>=0)&& (temp
a[j+1]=a[j];
j–; // 次序比较和移动,顺次将元素后移动一个方位
}
a[j+1]=temp;//元素后移后要刺进的方位就空出了,找到该方位刺进
}
}
我认为是一位刺进排序的算法时刻功率优于冒泡排序。最近在翻看《数据结构》发现书中介绍冒泡与刺进排序的时刻都是n*n,也便是n的平方。莫非是冒泡和刺进排序功率是相同的。可是问题为什么处理了,一年多上市出售也没有发现问题。咱们的细细研究一下。
排序的最极点状况是逆序,那么就选用逆序来测验一下两种算法。渠道运用VC6.0。
#include
void bubble_sort(int a[], int n);
void bubble_sort(int a[], int n)
{
int i, j, temp;
for (j = 0; j < n – 1; j++)
for (i = 0; i < n – 1 – j; i++)
{
if(a[i] > a[i + 1])
{
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
}
int main( )
{
int i;
int sort[6]={5,4,3,2,1,0};
bubble_sort( sort, sizeof( sort)/sizeof(int) );
for( i =0 ; i < sizeof( sort)/sizeof(int); i++ )
{
printf( " %d ", sort[i]);
}
printf("\n");
return 0;
}
咱们运用一个彻底逆序的数组作为测验样本。sort[6] = {5,4,3,2,1,0}; 程序运转成果彻底正确,从小到大排序。
咱们能够在bubble_sort(int a[], int n)增加代码计算出比较次数和**次数。
#include
int COMP_COUNT = 0;
int SWAP_COUNT = 0;
void bubble_sort(int a[], int n);
void bubble_sort(int a[], int n)
{
int i, j, temp;
for (j = 0; j < n – 1; j++)
for (i = 0; i < n – 1 – j; i++)
{
COMP_COUNT++;
if(a[i] > a[i + 1])
{
SWAP_COUNT +=3; //**计数器
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
}