“The only simple truth is that there is nothing simple in this complex universe. Everything relates. Everything connects”— Johnny Rich, The Human Script
介绍
机器学习的首要运用之一是对随机进程建模。机器学习中一些随机进程的比如如下:
●泊松进程:用于处理等待时刻以及行列。
●随机散步和布朗运动进程:用于买卖算法。
●马尔可夫决议计划进程:常用于核算生物学和强化学习。
●高斯进程:用于回归和优化问题(如,超参数调优和主动机器学习)。
●自回归和移动均匀进程:用于时刻序列剖析(如,ARIMA模型)。
在本文中,我将简要地向你介绍这些随机进程。
历史背景
随机进程是咱们日常日子的一部分。随机进程之所以如此特别,是由于随机进程依赖于模型的初始条件。在上个世纪,许多数学家,如庞加莱,洛伦兹和图灵都被这个论题所招引。
现在,这种行为被称为确认性混沌,它与真实的随机性有着天壤之别的规划边界。
由于爱德华·诺顿·洛伦兹的奉献,混沌体系的研讨在1963年取得了突破性发展。其时,洛伦兹正在研讨怎么改善天气预报。洛伦兹在他的剖析中注意到,即使是大气中的细小扰动也能引起气候变化。
洛伦兹用来描绘这种状况的一个闻名的短语是:
“A butterfly flapping its wings in Brazil can produce a tornado in Texas”
(在巴西,一只蝴蝶扇动翅膀就能在德克萨斯州制作龙卷风)
— Edward Norton Lorenz
(爱德华·诺顿·洛伦兹)
这便是为什么今日的混沌理论有时被称为“蝴蝶效应”。
分形学
一个简略的混沌体系的比如是分形(如图所示)。分形是在不同标准上不断重复的一种形式。由于分形的缩放方法,分形不同于其他类型的几何图形。
分形是递归驱动体系,能够捕获混沌行为。在现实日子中,分形的比如有:树、河、云、贝壳等。

图1:MC. Escher,Smaller and Smaller[1]
在艺术范畴有许多自相似的图形。毫无疑问, MC. Escher是最闻名的艺术家之一,他的著作创意来自数学。事实上,在他的画中重复呈现各种不或许的物体,如彭罗斯三角形和莫比乌斯带。在"Smaller and Smaller"中,他也重复运用了自相似性(图1)。除了蜥蜴的外环,画中的内部图画也是自相似性的。每重复一次,它就包括一个有一半标准的仿制图画。
确认性和随机性进程
有两种首要的随机进程:确认性和随机性。
在确认性进程中,假如咱们知道一系列事情的初始条件(起始点),咱们就能够猜测该序列的下一步。相反,在随机进程中,假如咱们知道初始条件,咱们不能彻底确认接下来的进程是什么。这是由于这个进程或许会以许多不同的方法演化。
在确认性进程中,一切后续进程的概率都为1。另一方面,随机性随机进程的状况则否则。
任何彻底随机的东西对咱们都没有任何用途,除非咱们能识别出其间的形式。在随机进程中,每个独自的事情都是随机的,虽然能够识别出衔接这些事情的躲藏形式。这样,咱们的随机进程就被揭开了奥秘的面纱,咱们就能够对未来的事情做出精确的猜测。
为了用统计学的术语来描绘随机进程,咱们能够给出以下界说:
●观测值:一次实验的成果。
●整体:一切或许的观测值,能够记为一个实验。
●样本:从独立实验中搜集的一组成果。
例如,抛一枚均匀硬币是一个随机进程,但由于大数规律,咱们知道,假如进行很多的实验,咱们将得到大约相同数量的正面和不和。
大数规律指出:
“跟着样本规划的增大,样本的均值将更挨近整体的均值或期望值。因而,当样本容量趋于无量时,样本均值收敛于整体均值。重要的一点是样本中的观测有必要是互相独立的。”
–Jason Brownlee
随机进程的比如有股票市场和医学数据,如血压和脑电图剖析。
泊松进程
泊松进程用于对一系列离散事情建模,在这些事情中,咱们知道不同事情产生的均匀时刻,但咱们不知道这些事情切当在何时产生。
假如一个随机进程能够满意以下条件,则能够以为它归于泊松进程:
●事情互相独立(假如一个事情产生,并不会影响另一个事情产生的概率)。
●两个事情不能同时产生。
●事情的均匀产生比率是稳定的。
让咱们以停电为例。电力供货商或许会宣扬均匀每10个月就会断电一次,但咱们不能精确地说出下一次断电的时刻。例如,假如产生了严重问题,或许会接连停电2-3天(如,让公司需要对电源供给做一些调整),以便在接下来的两天持续运用。
因而,关于这种类型的随机进程,咱们能够适当确认事情之间的均匀时刻,但它们是在随机的间隔时刻内产生的。
由泊松进程,咱们能够得到一个泊松散布,它能够用来推导出不同事情产生之间的等待时刻的概率,或许一个时刻段内或许产生事情的数量。
泊松散布能够运用下面的公式来建模(图2),其间k表明一个时期内或许产生的事情的预期数量。
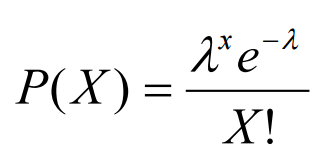
图2:泊松散布公式[3]
一些能够运用泊松进程模仿的现象的比如是原子的放射性衰变和股票市场剖析。
随机散步和布朗运动进程
随机散步是能够在随机方向上移动的恣意离散步的序列(长度总是相同,图3)。随机散步能够产生在任何维度空间中(如:1D,2D,nD)。

图3:高维空间[4]中的随机散步
现在我将用一维空间(数轴)向您介绍随机散步,这儿解说的这些概念也适用于更高维度。
咱们假定咱们在一个公园里,咱们看到一只狗在寻觅食物。它现在在数轴上的方位为0,它向左或向右移动找到食物的概率持平(图4)。
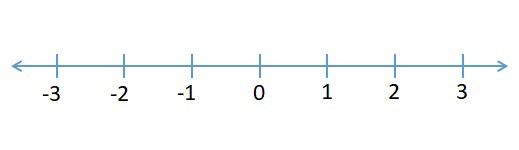
图4:数轴[5]
现在,假如咱们想知道在N步之后狗的方位是多少,咱们能够再次运用大数规律。运用这个规律,咱们会发现当N趋于无量时,咱们的狗或许会回到它的起点。无论怎么,此刻这种状况并没有多大用途。
因而,咱们能够测验运用均方根(RMS)作为间隔衡量(首要对一切值求平方,然后核算它们的均匀值,最终对成果求平方根)。这样,一切的负数都变成正数,均匀值不再等于零。
在这个比如中,运用RMS咱们会发现,假如咱们的狗走了100步,它均匀会从原点移动10步(√100=10)。
如前面所述,随机散步用于描绘离散时刻进程。相反,布朗运动能够用来描绘接连时刻的随机散步。









